◆詳細プロフィールはココ ◆YouTube はじめました
最新記事 by Ayaka (全て見る)
※コンテンツの無断転載禁止(リンク歓迎)
この動画では、小学生でも分かるように「シュレディンガーの猫」について解説しています。
まだ、1年前にアップされた動画なのに、100万回近くも再生されていてびっくり!ボーアの「この世界は実際に見てみるまで、どうなっているか分からない」という常識を壊すコペンハーゲン解釈について、「猫は可愛いという解釈は世界共通のようです」とうまく締めくくっているのが最高に好き
.

よく量子力学の話をしていると、シュレディンガーの猫の話をされるのですが、それよりも知ってほしいのはシュレディンガー方程式。
方程式と聞くと「うわー、無理!」みたいな顔をされることが多いものの、こちらも、大学物理の方程式を解いてもらおうとは思っていません。
ガイドをしていても、「興味深いけど全ては覚え切れない」と言われることがありますが、私が10ヶ月ほど専門スクールに通って、その時から今にかけて身につけた内容をお客さまが一日で習得されたら、私の立つ瀬がないですからね
ということで、今回は、この世の真理を数式にした【シュレディンガー方程式】が分かった気になるような記事を書いていこうと思います。

1. はじめに:物質の根源に迫る鍵
私たちが日常的に触れている世界をさらに細かく見ると、まったく異なるルールによって支配されるミクロの世界に入っていきます。そのミクロの世界を扱う理論が量子力学。この理論を読み解くうえで特に重要な役割を果たしているのが、オーストリアの物理学者エルヴィン・シュレディンガーが1926年に提唱した「シュレディンガー方程式」です。
この方程式は、電子などのミクロな粒子が時間と空間の中でどのように存在し、振る舞うかを記述する基本法則であり、古典力学(一般の物理法則)におけるニュートンの運動方程式に相当するもの。物理においては超基本の式なので、物理・工学などの理系学部では大学1〜2年生で学びはじめます。
2. 時間依存型と時間非依存型
シュレディンガー方程式には2つのタイプがあります。ひとつは、時間依存型。これは、時間がたつにつれて量子がどう動くのかを追いかける式です。たとえば、防犯カメラの映像みたいなもので、「この時間にはここにいた」「数分後はあっちに行った」と、動きをずっと記録していきます。
そしてもうひとつが、時間非依存型。こっちは時間は関係なく、「この粒は、いつ見てもこういう状態にある」という一枚の写真のようなもの。動いてる様子は見えないけど、その瞬間の特徴(エネルギーなど)をバシッと写し取っています。つまり、防犯カメラ(時間依存型)は「動き」を、写真(時間非依存型)は「その場の状態」を見てる感じ。どっちも同じ場所のことを調べてるけど、見る角度が違うんです。式は、時間依存型のほうが複雑です。
3. さらに次元によって式は変わる
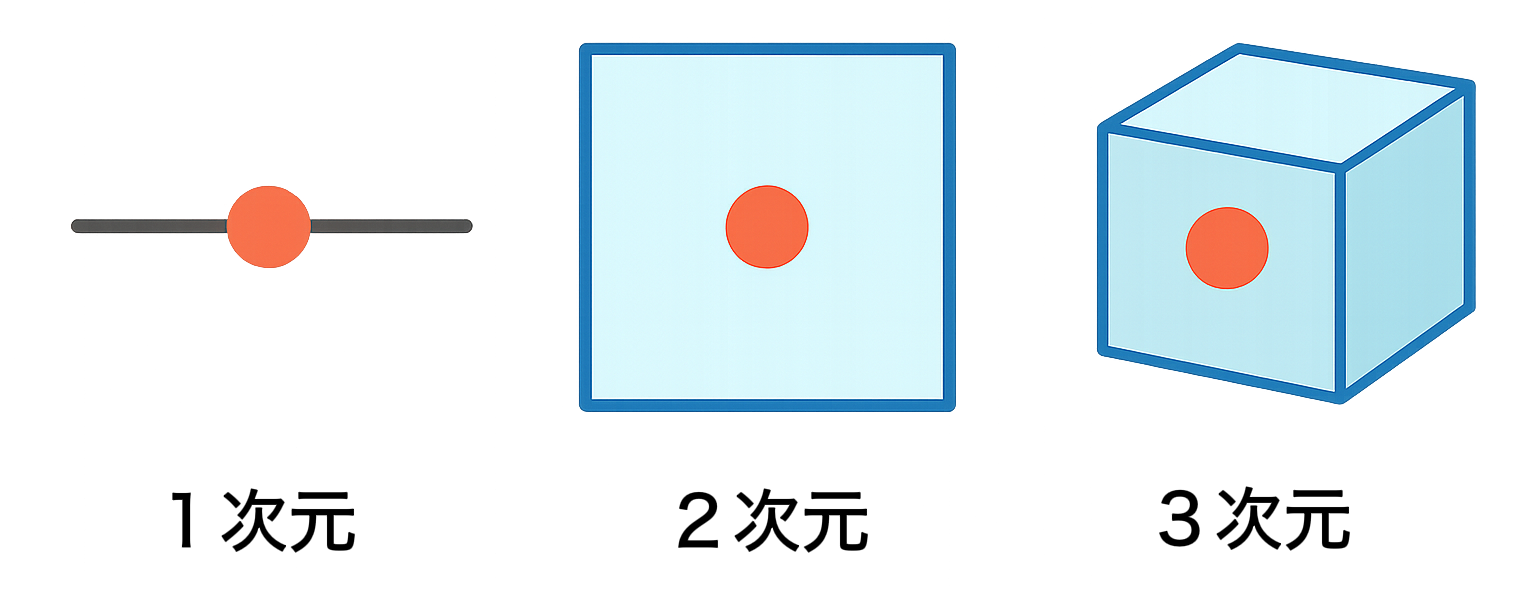
シュレディンガー方程式には、先ほど触れた「時間」以外にも「次元」という重要な観点があり、状況に応じて使い分けられます。皆さんもなんとなくご存知の通り、1次元は線の上、2次元は平面、3次元は立体空間を意味します。次元が増えるほど方程式は複雑になり、現実に近い3次元では、もはや手計算では追いつかず、コンピュータが必須。
4次元以上になると「次元の呪い」と呼ばれるほど計算量が急増し、スパコンでも難しい世界になります。さらに10次元や11次元といった高次元は、超ひも理論などの理論物理でしか使われません。でも実は、ひとつひとつを丁寧に分解していけば、意外とシンプルな考え方の組み合わせでもあります。
ということで、時間依存型の式を見てみましょう。
.
こちらは、基本的な形である【時間依存型のシュレディンガー方程式(time-dependent Schrödinger equation)】です。
この方程式は「波動関数 ψ が時間とともにどのように変化していくか」を決定するもの。ここで登場する記号の意味を一つずつ説明してみます。
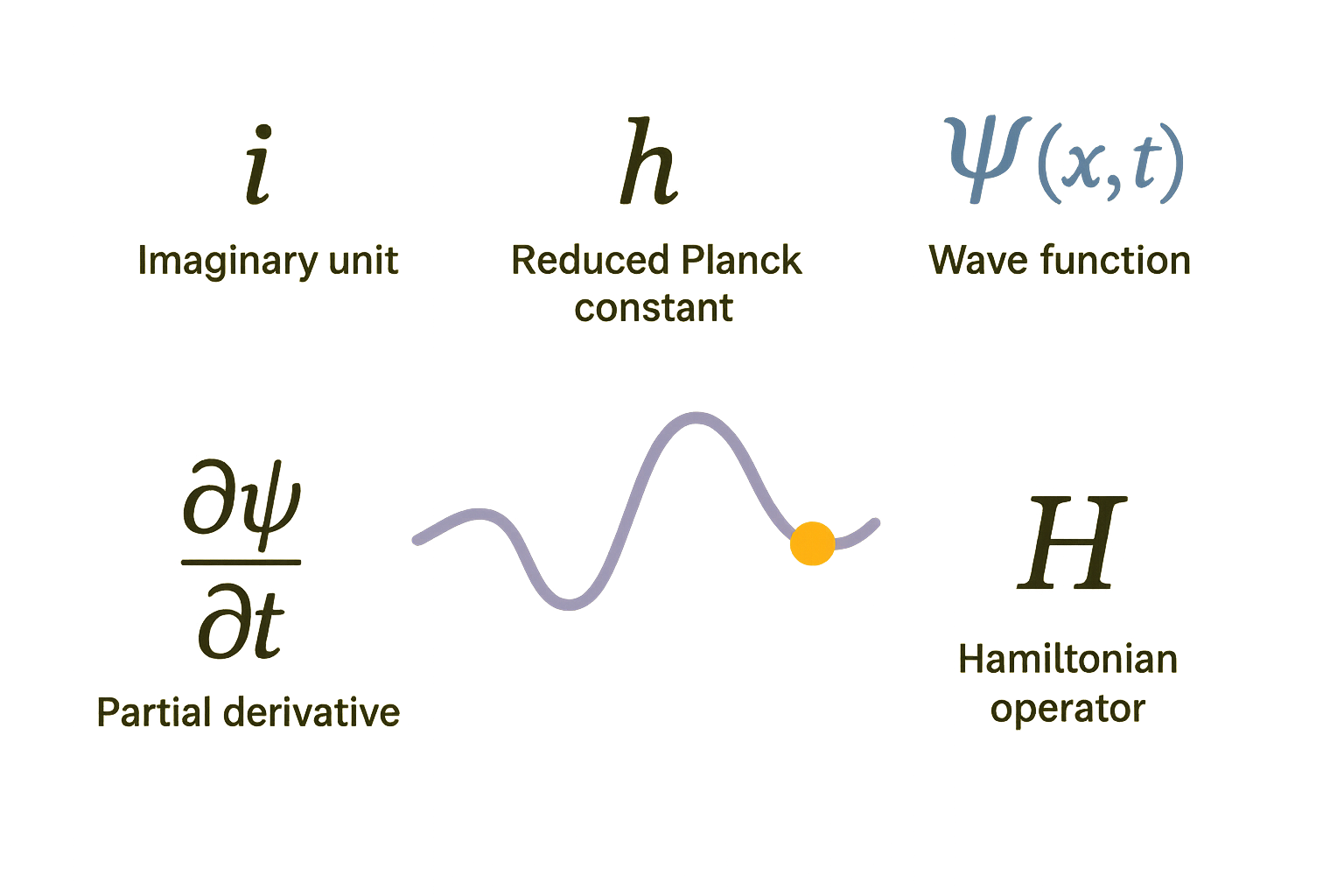
◆ i … 虚数単位(i² = -1)
高校数学でも出てくるお馴染み?の虚数。これは、“かけるとマイナスになる不思議な数”です。ふつう、2×2=4 みたいに、同じ数をかけるとプラスになりますが、虚数の場合、i × i = -1 というルールを持っています。実際の数直線では表せないけど、量子力学や電気の世界ではとても役立つ数です。
◆ ħ(エイチバー)… 換算プランク定数
これは「h」というプランク定数を2πで割ったもので、ħ = h / (2π) という関係になります。プランク定数は、お金にたとえると0.小数点の後に「0」が33個+6626円くらい。つまり、とても小さな量子の変化を測るための“目盛り”みたいなもの。ħは、電子や光などのミクロの世界でルールを決める物差しで、量子力学の計算ではいつも出てきます。
◆ ψ(x,t) … 波動関数
位置 x と時間 t における粒子の状態を表します。この関数を使えば、「電子がこのあたりに存在する確率が高い」といった情報を得ることができますが、波動関数は古典物理学には存在しない量なので理解が難しい。この関数そのものが見えるわけじゃなくて、意味があるのは“どう分布してるか”という形だけです。|ψ(x,t)|² は、「時刻 t において、粒子が位置 x に存在する確率密度」を表します。
◆ ∂ψ/∂t … ψ の時間微分
これは時間に関してどのように変化するかを示すもので、シンプルに言うならば、粒子の状態が時間とともにどれくらい変わっているかを表す記号です。たとえば、朝と夜で空の色が変わるように、粒の位置の予想も時間とともに変わります。つまり、一瞬ごとの変化のスピード=瞬間的な変化を計算する道具です。数学的には「偏微分」と言います。
◆ Ĥ … ハミルトニアン演算子
量子力学における、エネルギーのしらべ役。粒子が持つ運動エネルギーと位置エネルギーをすべて合計して、その粒がどれくらいのエネルギー状態にあるのかを調べるための道具です。波動関数にこの Ĥ を使うことで、「その粒子がどんなふうに振る舞うか」を計算できるようになります。


























